在Python中数字类型分为:整形、布尔型、浮点型以及复数型
创建int类型的对象
int类型通常为数字,创建int类型的方式有两种,在创建的时候两边不需要加单引号或上引号。
第一种创建int类型方式:
>>> age = 18
>>> type(age)
<class 'int'>
第二种创建int类型方式:
>>> age = int(18)
>>> type(age)
<class 'int'>
以上两种创建int对象的方式都是可行的,但是他们也是有本质上的区别,第一种方式实际上会转换成第二种方式,然后第二种方式会把括号内的数据交给init这个构造方法,构造方法是int类的,然后构造方法会在内存中开辟一块空间用来存放数据,但实际上我们在用时候是没有任何区别的。
构造方法每个数据类型中都会有,这是Python内部所定义的,如下图所示:
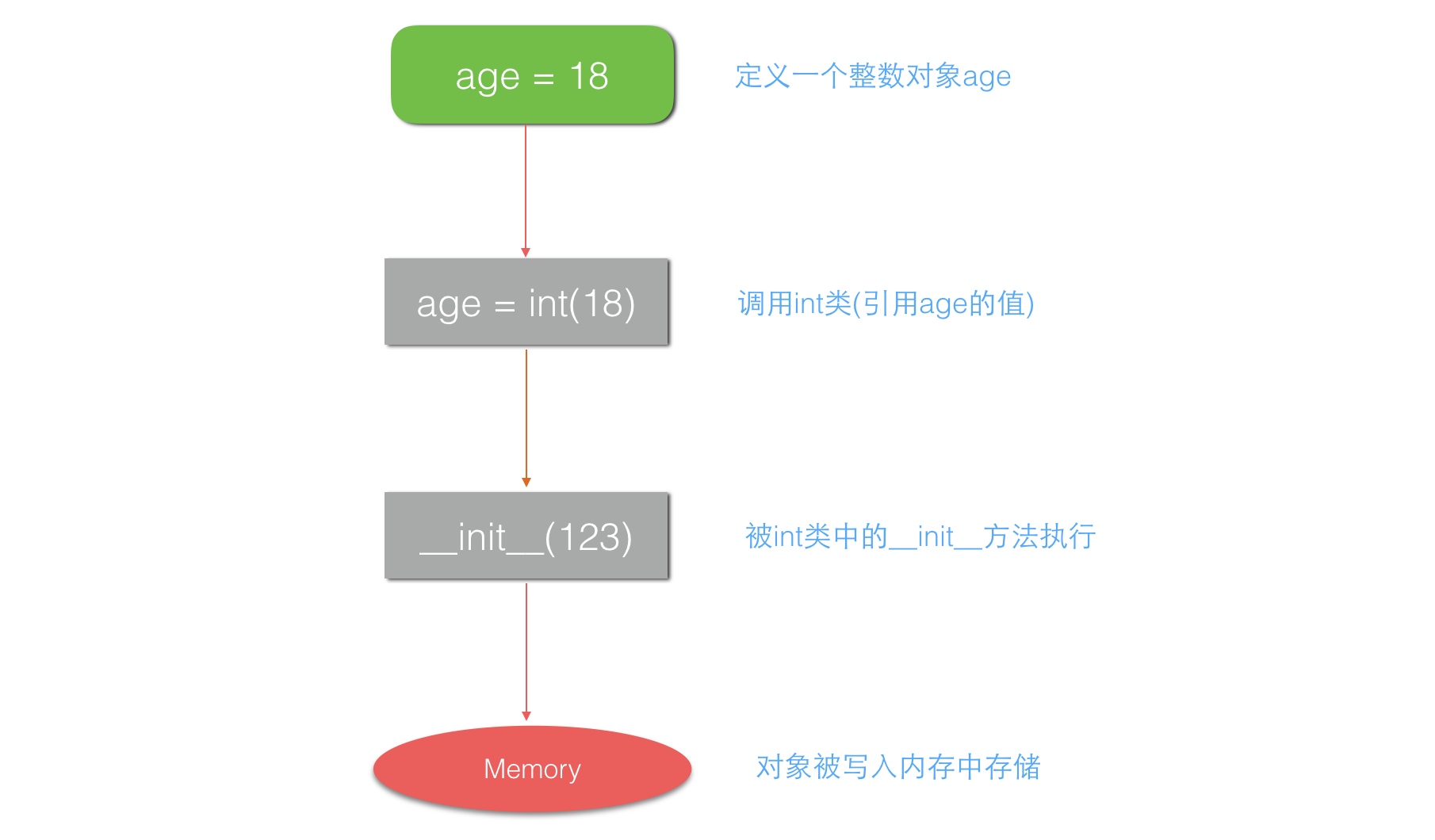
我们来看看__init__方法的具体情况:
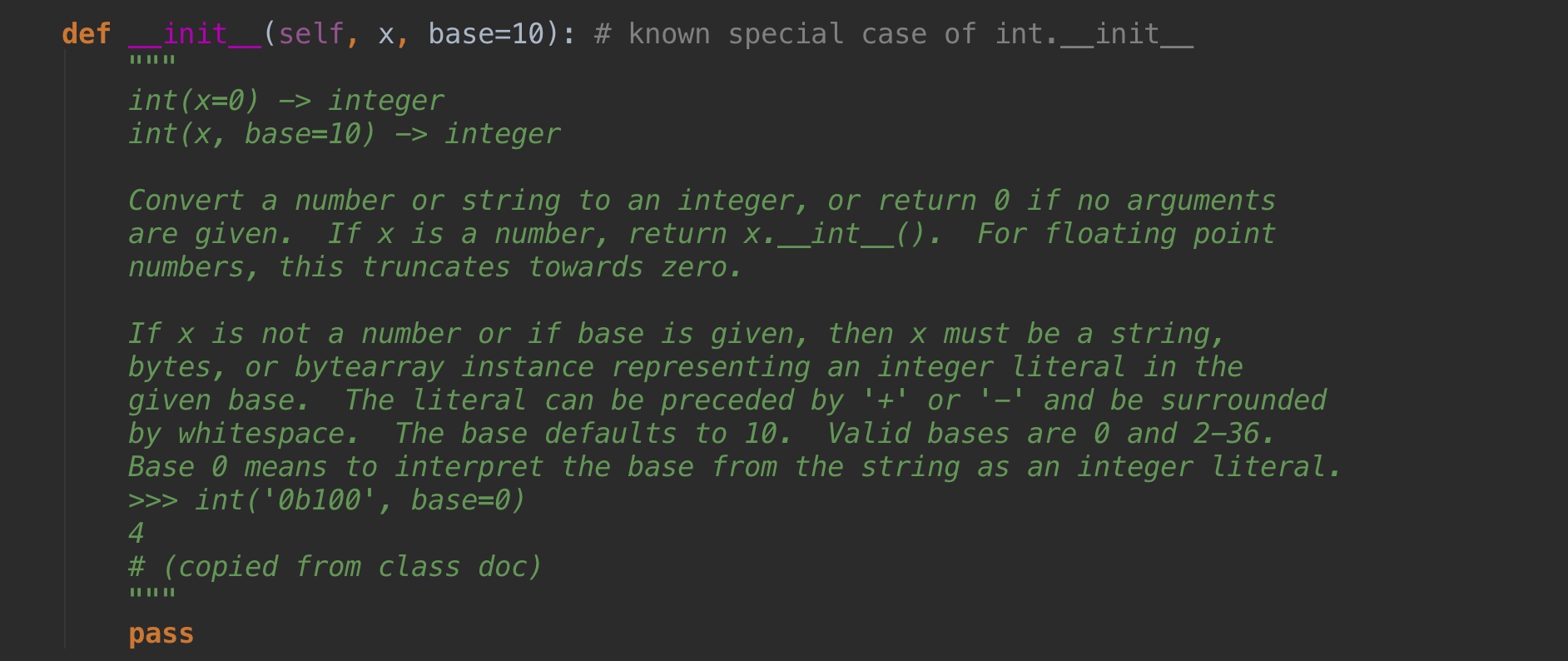
从上图源码中可以看出__init__的方法有两个参数,其中base=10是可选的参数,x是我们对象的值,base=10其实就是说把我们的值(默认二进制)以十进制的方式输出出来,通过下面的实例你可以理解:
>>> int('100', base=10)
100
>>> int('0b100', base=0)
4
通过int可以将一个数字的字符串变成一个整数,并且如果你指定了第二个参数,还可以将进制数转换为整数:
# 将数字字符串转换为整数,数字字符串通过进制转换为整数
>>> int('18'), int('100', 8)
(18, 64)
# 将进制数转换为整数
>>> int('0x40',16),int('0b1000000',2)
(64, 64)
Python中的整数属于int类型,默认用十进制表示,此外也支持二进制,八进制,十六进制表示方式。
进制转换
尽管计算机只认识二进制,但是为了迎合我们的习惯,python中的数字默认还是十进制。还提供了一些方法来帮助我们做转换。比如是进制转换为二进制使用bin方法,在转换结果前面还会加上'0b'表示是一个二进制书。
既然十进制可以转换为二进制,那么其实使用同样的原理也可以转换为其他进制,python也为我们提供了十进制转换成八进制和十六进制的方法,分别是oct和hex。八进制前面以'0o'标示,十六进制以'0x'表示。
>>> bin(10)
'0b1010'
>>> oct(10)
'0o12'
>>> hex(10)
'0xa'
int内部优化机制
如下图中我们可以很清楚的看到int类型在创建对象时内存空间分配的情况
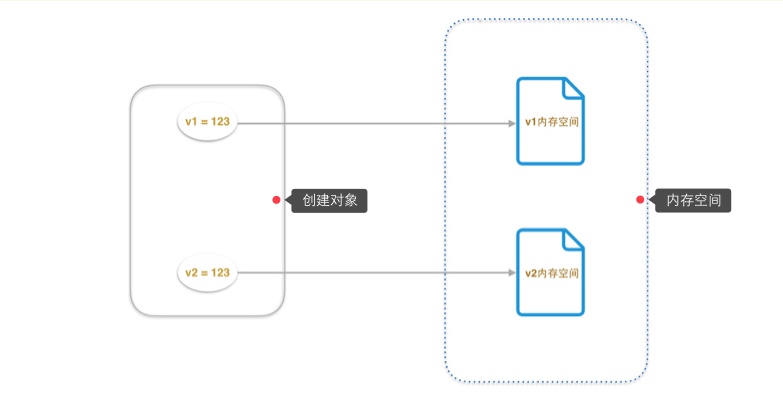
当我们创建第一个对象v1的时候会在内存中开辟一块空间作为存放v1对象的值,当我们创建第二个对象v2的时候也会在内存中开辟一块空间来作为v2对象的值,那如果这样说,那是不是说对象v1和v2的内存地址是两块呢?我们通过下面的实例可以得到答案:
Python 3.5.1 (default, Dec 26 2015, 18:08:53)
[GCC 4.2.1 Compatible Apple LLVM 7.0.2 (clang-700.1.81)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> v1=123
>>> v2=123
>>> id(v1), id(v2)
(4549969744, 4549969744)
通过上面的结果我们可以看到var1和var2的内存地址是相同的,就代表他们的值是使用的同一块空间,所以当两个或者多个对象的值都是同一个的时候,那么这些对象都会使用同一个内存地址,这里的值是是有范围的,默认范围是-5~257,得到这个结论之后我们继续往下看:
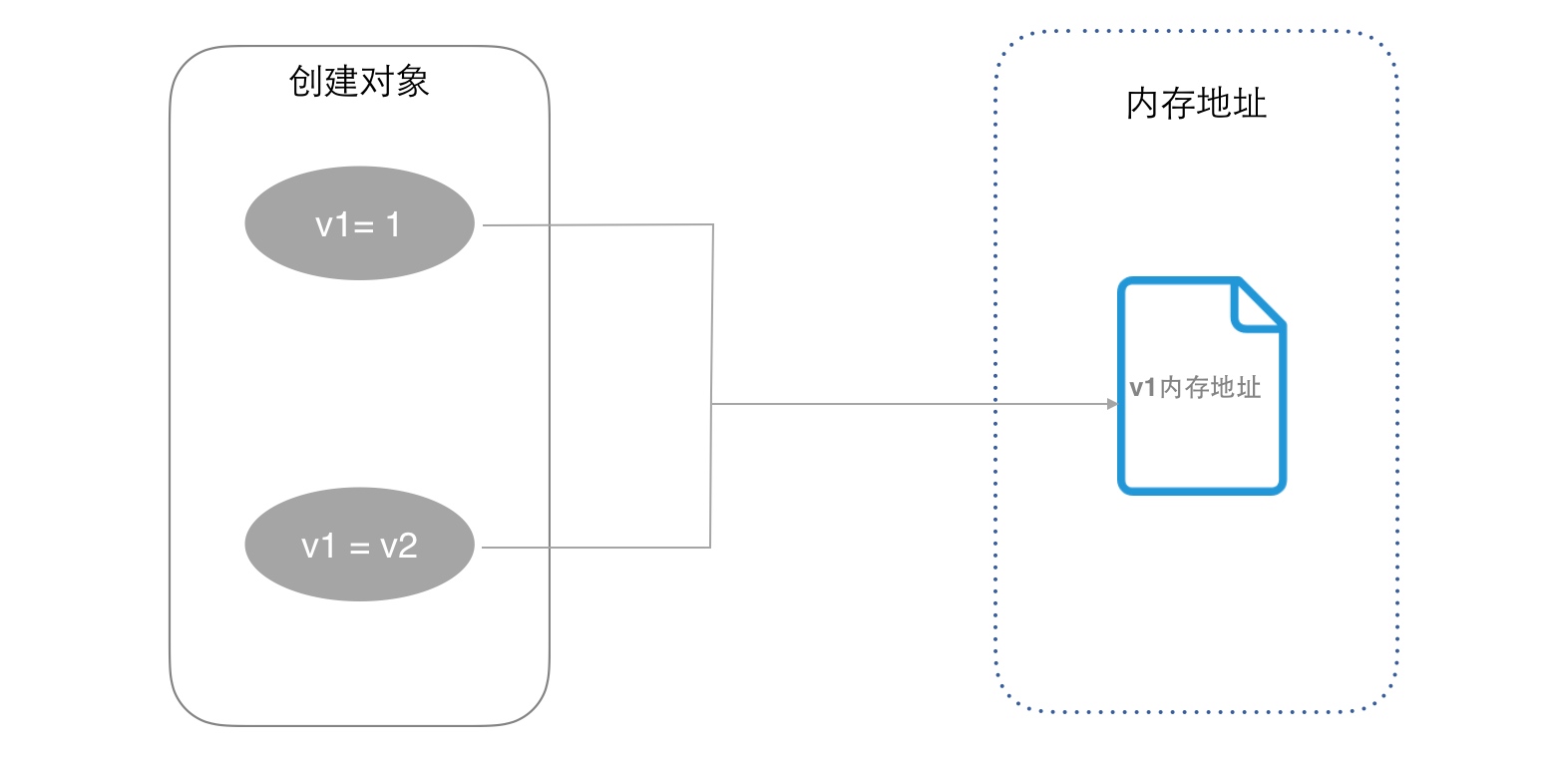
这张图我们同样创建了两个对象,但是唯一不同的是我把第一个创建的对象的值作为第二个对象的值,这里他们肯定使用的是同一个内存地址,但是如果我把第一个对象的值改动了呢:
>>> v1 = 1; v2 = v1
>>> id(v1), id(v2)
(4462839824, 4462839824)
>>> v1 = 2
>>> id(v1), id(v2)
(4462839856, 4462839824)
刚才我们上面说过-5~257这个范围内对象的值都会引用同一块内存地址,我们可以通过下面的实验来验证一下:
>>> v1 = 54188
>>> v2 = 54188
>>> id(v1), id(v2)
(4517809680, 4517807888)
通过上面试验证明我们的结论是没有问题的,注意我上面的实例都是在Python3.5上面执行的,v1和v2两个对象的值同样是54188,但是他们的内存地址就是不一样,这就是Python在内部做的优化,它把-5~257这个范围内的数字定义为可多对象引用。
数字类型的长度限制
跟C语言不同,Python的长整数没有指定位宽,即:Python没有限制长整数数值的大小,但实际上由于机器内存有限,我们使用的长整数数值不可能无限大。
注意: 自从Python2.2起,如果整数发生溢出,Python会自动将整数数据转换为长整数,所以如今在长整数数据后面不加字母L也不会导致严重后果了。
数字类型在Python2.7里面是分整型和长整型,也就是说如果你的数字大到一定的范围,那么Python会把它转换为长整形,一个数字类型包含32位,可以存储从-2147483648到214483647的整数。
一个长整型(long)会占用更多的空间,64位的可以存储-922372036854775808到922372036854775808的整数。
所以不同的操作系统中数据的长度是有限制范围的,就好像32位系统最多支持4GB内存一样。
Python3里long型已经不存在了,而int型可以存储到任意大小的整型,甚至超过64位。
Python内部对整数的处理分为普通整数和长整数,普通整数长度为机器位长,通常都是32位,超过这个范围的整数就自动当长整数处理,而长整数的范围几乎完全没限制,如下:
Python2.7.x
Python 2.7.10 (default, Jul 14 2015, 19:46:27)
[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.39)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> v1 = 54188
>>> v1
54188
>>> v1 = 10 ** 20
>>> v1
100000000000000000000L
>>> type(v1)
<type 'long'>
Python3.5.x
Python 3.5.1 (default, Dec 26 2015, 18:08:53)
[GCC 4.2.1 Compatible Apple LLVM 7.0.2 (clang-700.1.81)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> v1 = 54188
>>> v1
54188
>>> v1 = 10 ** 20
>>> v1
100000000000000000000
>>> type(v1)
<class 'int'>
布尔型
在Python的世界里面有一个叫布尔值的东西,布尔类型其实就是数字0和1的变种而来,即真(True/0)或假(False/1),实际上就是内置的数字类型的子类而已。
在其他的配置或者语言里面,我们都知道把某个东西打开需要把他调试为True,关闭则设置为False。
在Python里面也是一样True就代表为真,条件成立;False就代表为假,条件不成立;1代表为真,0
代表假。
bool型只有两个值:True和False,之所以将bool值归类为数字,是因为我们也习惯用1表示True,0表示False。
>>> if 1: print("1 is True")
...
1 is True
>>> if not 0: print("0 is False")
...
0 is False
>>> if True: print("True is 1")
...
True is 1
>>> if not False: print("False is 0")
...
False is 0
你还可以使用布尔值进行加减法,虽然从来没在任何代码中见过这种形式:
>>> True + 99 """ = 1 + 99 """
100
>>> 101 - False """ = 101 - 1 """
101
浮点型
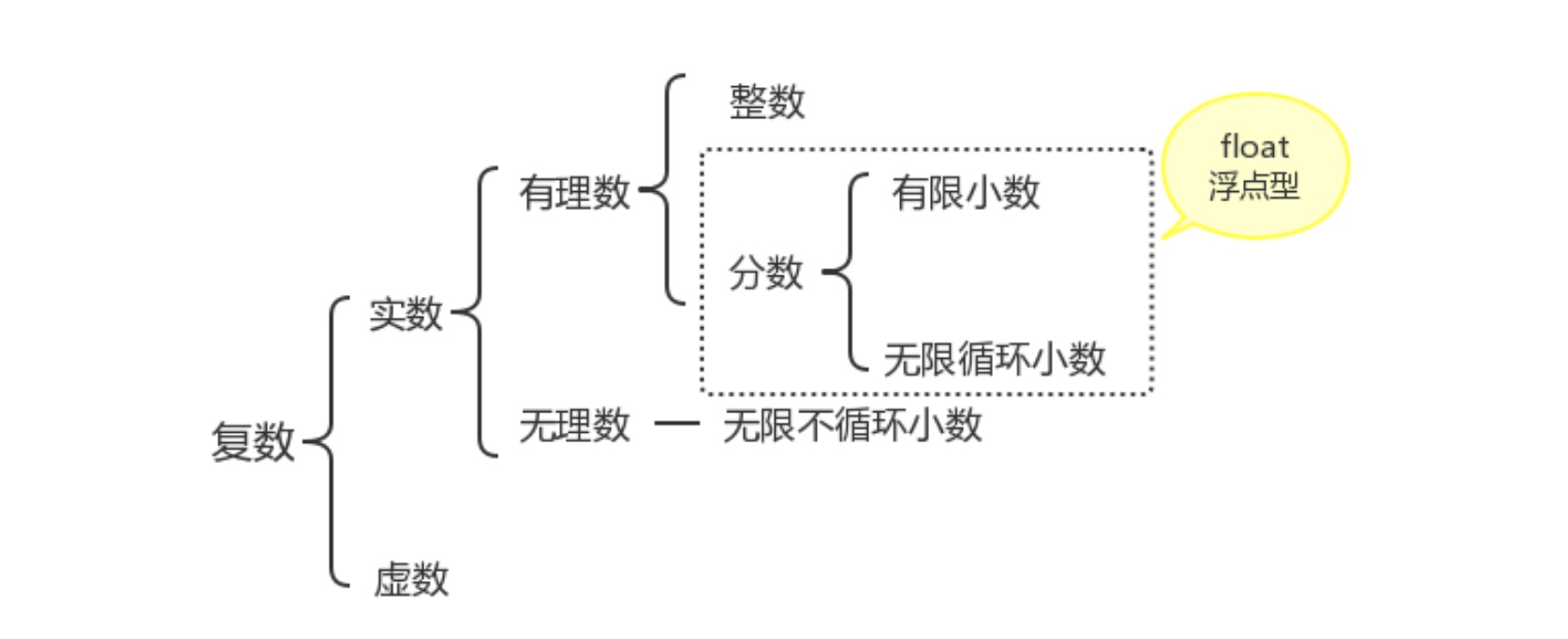
浮点数是属于有理数中某特定子集的数的数字表示,在计算机中用以近似表示任意某个实数。具体的说,这个实数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2)的整数次幂得到,这种表示方法类似于基数为10的科学计数法。
浮点数用来处理实数,即带有小数的数字。类似于C语言中的double类型,占8个字节(64位),其中52位表示底,11位表示指数,剩下的一位表示符号。
在运算中,整数与浮点数运算的结果也是一个浮点数。
为什么要叫做float浮点型:
浮点数也就是小数,之所以称为浮点数,是因为按照科学记数法表示时,一个浮点数的小数点位置是可变的,比如: 1.23 * 109和 12.3 * 108是相等的。
浮点数可以用数学写法,如1.23,3.14,-9.01,等等。但是对于很大或很小的浮点数,就必须用科学计数法表示,把10用e替代:1.23*109就是1.23e9,或者12.3e8,0.000012可以写成1.2e-5,等等。
整数和浮点数在计算机内部存储的方式是不同的,整数运算永远是精确的而浮点数运算则可能会有四舍五入的误差。
关于小数不精准问题:
Python默认的是17位精度,也就是小数点后16位,尽管有16位,但是这个精确度却是越往后越不准的。
首先,这个问题不是只存在在python中,其他语言也有同样的问题;其次,小数不精准是因为在转换成二进制的过程中会出现无限循环的情况,在约省的时候就会出现偏差。
比如:11.2的小数部分0.2转换为2进制则是无限循环的00110011001100110011...
单精度在存储的时候用23bit来存放这个尾数部分(前面9比特存储指数和符号);同样0.6也是无限循环的。
这里有一个问题,就是当我们的计算需要使用更高的精度(超过16位小数)的时候该怎么做呢?
#借助decimal模块的“getcontext“和“Decimal“ 方法
>>> a = 3.141592653513651054608317828332
>>> a
3.141592653513651
>>> from decimal import *
>>> getcontext()
Context(prec=50, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[FloatOperation], traps=[InvalidOperation, DivisionByZero, Overflow])
>>> getcontext().prec = 50
>>> a = Decimal(1)/Decimal(3)#注,在分数计算中结果正确,如果直接定义超长精度小数会不准确
>>> a
Decimal('0.33333333333333333333333333333333333333333333333333')
>>> a = '3.141592653513651054608317828332'
>>> Decimal(a)
Decimal('3.141592653513651054608317828332')
#不推荐:字符串格式化方式,可以显示,但是计算和直接定义都不准确,后面的数字没有意义。
>>> a = ("%.30f" % (1.0/3))
>>> a
'0.333333333333333314829616256247'
简单举例浮点数:
>>> age = 18
>>> print(type(age))
<class 'int'>
>>> float_age = float(age)
>>> float_age
18.0
>>> print(type(float_age))
<class 'float'>
具体更多功能查看帮助:
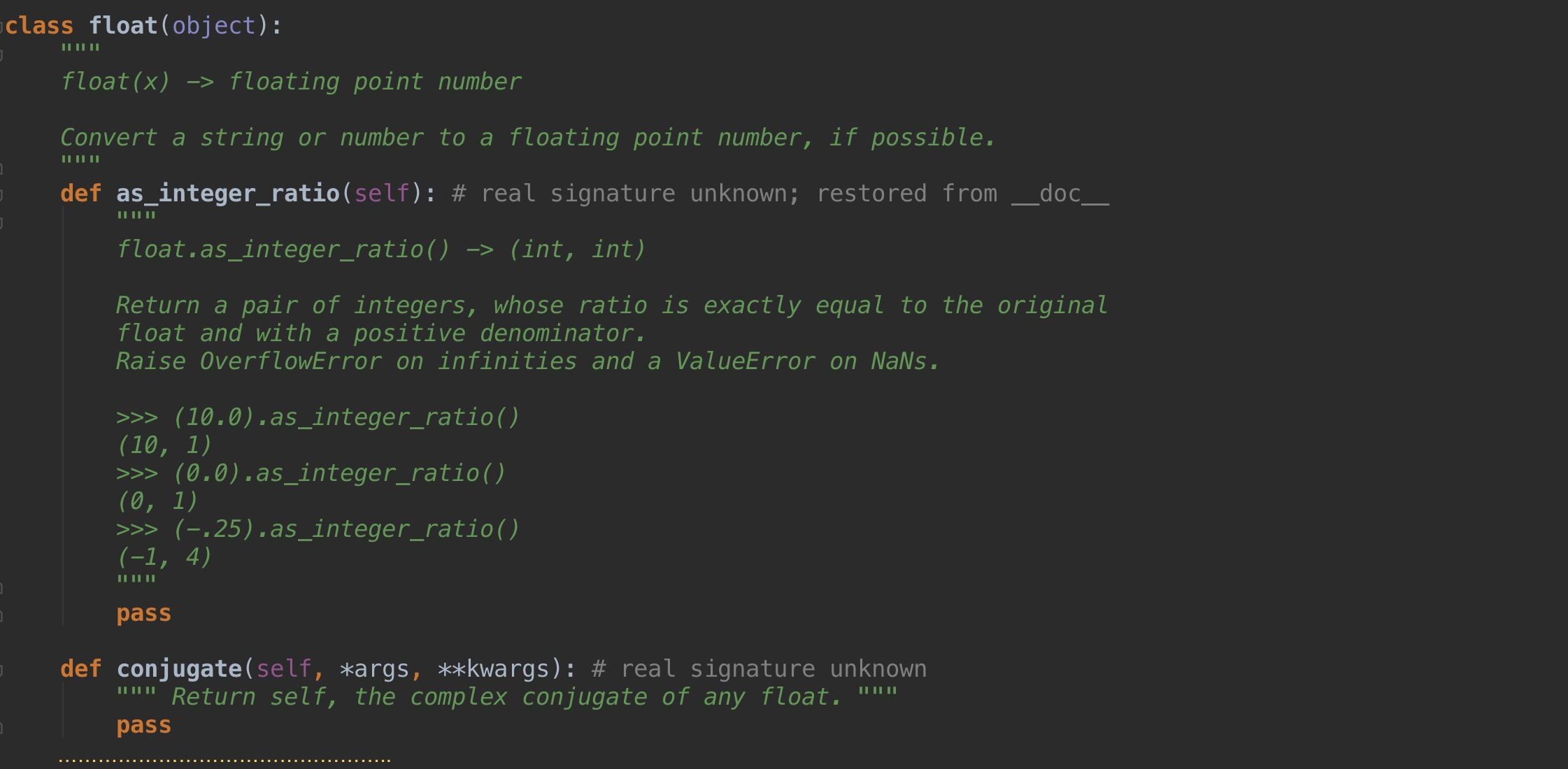

复数型
复数由实数部分和虚数部分组成,一般形式为a+bi,其中的x是复数的实数部分,y是复数的虚数部分,这里的x和y都是实数。
要了解复数,其实关于复数还需要先了解虚数。虚数(就是虚假不实的数):平方为复数的数叫做虚数。
复数是指能写成如下形式的数a+bj,这里a和b是实数,j是虚数单位(即-1开根)。在复数a+bj中,a称为复数的实部,b称为复数的虚部(虚数是指平方为负数的数),j称为虚数单位。
当虚部等于零时,这个复数就是实数;当虚部不等于零时,这个复数称为虚数。
>>> a = complex(2, 4)
>>> b = 3 - 5j
>>> a
(2+4j)
>>> b
(3-5j)
>>> type(a);type(b)
<class 'complex'>
<class 'complex'>
两头牛背上的架子称为轭,轭使两头牛同步行走。共轭即为按一定的规律相配的一对.这是作者的解释,很形象,不过还是来看他的数学含义吧!
所谓共轭复数,简单来说就是两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number). 关于x轴对称,就像两头牛平行的拉一部梨。
关于复数的一些方法
conjugate: 返回该复数的共轭复数
>>> a = 1 + 2j
>>> a.conjugate()
(1-2j)
real: 返回复数的实部
>>> a = 1 + 2j
>>> a.real
1.0
imag: 返回复数的虚部
>>> a = 1 + 2j
>>> a.imag
2.0
混合类型
所谓混合类型就是浮点数和整数进行运算,如下所示:
>>> 3.14159 + 10
13.14159
结果和我们想象中的一样,但是一个浮点数一个正整数它是怎么进行相加的呢?其实很简单,Python会把两个值转换为其中最复杂的那个对象的类型,然后再对相同类型运算。
比如上面的例子中,会先把10转换为10.0然后再与3.14159相加。
类型间的互相转换可以利用int(), float(), complex 。
到这里数据类型数字就都介绍完成了,左后说明一下整数比浮点数简单、浮点数比复数简单, 数字的运算会在运算符的知识点中统一介绍。

本文由 空心菜 创作,采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间为: Jun 3, 2018 at 08:26 am
